什么的湖面什么填词语
1、波涛起伏的湖面。
2、微波粼粼的湖面。
3、微波起伏的湖面。
4、波光粼粼的湖面。

扩展资料：
1、波涛起伏：[ bō tāo qǐ fú ]
基本解释：比喻情况万分危急。
2、微波粼粼：[ wēi bō lín lín ]
基本解释：微：细小；粼粼：细小的水波闪闪发光。 形容水石等很明净。
3、波光粼粼：[ bō guāng lín lín ]
基本解释：形容波光明净。波光：阳光或月光照在水波上反射过来的光。粼粼：形容水石明净。

初中常见的勾股数

常见组合

3，4，5 ： 勾三股四弦五

5，12，13 ： 5·21（12）记一生（13）

6，8，10： 连续的偶数

8，15，17 ： 八月十五在一起（17）

特殊组合

连续的勾股数只有3，4，5

连续的偶数勾股数只有6，8，10

20以内

3 4 5；5 12 13； 6 8 10；8，15，17；9 12 15

初中常见的勾股数有哪些

勾股数的概念

勾股数，又名毕氏三元数 。勾股数就是可以构成一个直角三角形三边的一组正整数。勾股定理：直角三角形两条直角边a、b的平方和等于斜边c的平方（a²+b²=c²）。

完全公式

a=m，b=(m^2/k-k) / 2，c=(m^2/k+k) / 2

其中m ≥3

当m确定为任意一个≥3的奇数时，k={1，m^2的所有小于m的因子}

当m确定为任意一个≥4的偶数时，k={m^2/2的所有小于m的偶数因子}

基本勾股数与派生勾股数可以由完全一并求出。例如，当m确定为偶数432时，因为k={432^2 / 2的所有小于432的偶数因子}= {2，4，6，8，12，16，18，24，32，36，48，54，64，72，96，108，128，144，162，192，216，288，324，384}，将m=432及24组不同k值分别代入b=(m^2 / k-k) / 2，c=(m^2 /k+k) / 2；即得直角边a=432时，具有24组不同的另一直角边b和斜边c，基本勾股数与派生勾股数一并求出。而勾股数的组数也有公式能直接得到。

在欧几里得的《几何原本》一书中给出勾股定理的以下证明。设△ABC为一直角三角形，其中A为直角。从A点划一直线至对边，使其垂直于对边。延长此线把对边上的正方形一分为二，其面积分别与其余两个正方形相等。

在这个定理的证明中，我们需要如下四个辅助定理：

如果两个三角形有两组对应边和这两组边所夹的角相等，则两三角形全等。（SAS）

三角形面积是任一同底同高之平行四边形面积的一半。

任意一个正方形的面积等于其二边长的乘积。

任意一个矩形的面积等于其二边长的乘积。

证明的思路为：从A点划一直线至对边，使其垂直于对边。延长此线把对边上的正方形一分为二，把上方的两个正方形，通过等高同底的三角形，以其面积关系，转换成下方两个同等面积的长方形。

设△ABC为一直角三角形，其直角为∠CAB。

其边为BC、AB和CA，依序绘成四方形CBDE、BAGF和ACIH。

画出过点A之BD、CE的平行线，分别垂直BC和DE于K、L。

分别连接CF、AD，形成△BCF、△BDA。

∠CAB和∠BAG都是直角，因此C、A和G共线，同理可证B、A和H共线。

∠CBD和∠FBA都是直角，所以∠ABD=∠FBC。

因为AB=FB，BD=BC，所以△ABD≌△FBC。

因为A与K和L在同一直线上，所以四边形BDLK=2△ABD。

因为C

A和G在同一直线上，所以正方形BAGF=2△FBC。

因此四边形BDLK=BAGF=AB²。

同理可证，四边形CKLE=ACIH=AC²。

把这两个结果相加，AB²+AC²=BD×BK+KL×KC

由于BD=KL，BD×BK+KL×KC=BD(BK+KC)=BD×BC

由于CBDE是个正方形，因此AB²+AC²=BC²，即a²+b²=c²。

此证明是于欧几里得《几何原本》一书第1.47节所提出的。

由于这个定理的证明依赖于平行公理，而且从这个定理可以推出平行公理，很多人质疑平行公理是这个定理的必要条件，一直到十九世纪尝试否定第五公理的非欧几何出现。

c语言中str是什么意思
str -- 通常，程序员喜欢用它作字符串变量名。它是 string（英文词、字符串的缩写）

Str函数，返回代表一数值的 Variant（String）。语法Str（number）必要的 number 参数为一 Long，其中可包含任何有效的数值表达式。说明当一数字转成字符串时，总会在前头保留一空位来表示正负。

扩展资料：

如果 number 为正，返回的字符串包含一前导空格暗示有一正号。使用 Format 函数可将数值转成必要的格式，如日期、时间、货币或其他用户自定义格式。与 Str 不同的是，Format 函数不包含前导空格来放置 number 的正负号。

注意 Str 函数只视句点 (.) 为有效的小数点。如果使用不同的小数点（例如，国际性的应用程序），可使用 CStr 将数字转成字符串。

广东省26个字母车牌是如下：

一、A——广州市

二、B——深圳市

三、C——珠海市
四、D——汕头市

五、E——佛山市

六、F——韶关市

七、G——湛江市

八、H——肇庆市

九、J——江门市

十、K——茂名市

十一、L——惠州市

十二、M——梅州市

十三、N——汕尾市

十四、P——河源市

十五、Q——阳江市

十六、R——清远市

十七、S——东莞市

十八、T——中山市

十九、U——潮州市

二十、V——揭阳市

二十一、W——云浮市

二十二、X——顺德区

二十三、Y——南海区

二十四、Z——香港澳门进入内地车辆

天门中断楚江开的楚江指的是什么意思
“天门中断楚江开”的“楚江”指的是：长江，古代长江中游地带属楚国，所以叫楚江。出自唐代李白的《望天门山》。《望天门山》是唐代大诗人李白于开元十三年（725年）赴江东途中行至天门山时所创作的一首七绝。
原文：
天门中断楚江开，碧水东流至此回。
两岸青山相对出，孤帆一片日边来。
创作背景：
《望天门山》是公元725年（开元十三年）李白初出巴蜀乘船赴江东经当涂（今属安徽）途中行至天门山，初次见到天门山时有感而作的。

正月，即为“建正”之月，在观象授时时代，斗柄回寅为春正，春正所在的月份即正月。历法建正，原是摄提纪论十二月建的概念。后经演变，亦用来指其它历法的首月。现通常指农历的第一个月。
夏历以春一月为正月，相当于在干支历建寅之月；商历以冬十二月为正月，相当于在干支历建丑之月；周历以冬十一月为正月，相当于在干支历建子之月；秦历以冬十月为正月，相当于在干支历建亥之月。这便是夏历建寅、商历建丑、周历建子、秦历建亥说法的由来，其实它们分属不同的历法，是对应关系。

众数是什么
众数是指在统计分布上具有明显集中趋势点的数值，代表数据的一般水平。也是一组数据中出现次数最多的数值，有时众数在一组数中有好几个。用M表示。主要应用于大面积普查研究之中。

众数定义

众数是样本观测值在频数分布表中频数最多的那一组的组中值，主要应用于大面积普查研究之中。

众数是在一组数据中,出现次数最多的数据，是一组数据中的原数据，而不是相应的次数。

一组数据中的众数不止一个，如数据2、3、-1、2、1、3中，2、3都出现了两次，它们都是这组数据中的众数。

一般来说，一组数据中，出现次数最多的数就叫这组数据的众数。

例如：1，2，3，3，4的众数是3。

但是，如果有两个或两个以上个数出现次数都是最多的，那么这几个数都是这组数据的众数。

例如：1，2，2，3，3，4的众数是2和3。

还有，如果所有数据出现的次数都一样，那么这组数据没有众数。

例如：1，2，3，4，5没有众数。

在高斯分布中，众数位于峰值。

一的大写是什么
壹：“一”的大写。人民币金额用到的中文大写汉字如下：零、壹、贰、叁、肆、伍、陆、柒、捌、玖、拾、佰、仟、万、亿。

人民币大写的正确写法还应注意以下几项：

一、中文大写金额数字到“元”为止的，在“元”之后、应写“整”（或“正”）字；在“角”之后，可以不写“整”（或“正”）字；大写金额数字有“分”的，“分”后面不写“整”（或“正”）字。

二、中文大写金额数字前应标明“人民币”字样，大写金额数字应紧接“人民币”字样填写，不得留有空白。大写金额数字前未印“人民币”字样的，应加填“人民币”三字，在票据和结算凭证大写金额栏内不得预印固定的“仟、佰、拾、万、仟、佰、拾、元、角、分”字样。

三、阿拉伯数字小写金额数字中有“0”时，中文大写应按照汉语语言规律、金额数字构成和防止涂改的要求进行书写。

四、阿拉伯小写金额数字前面均应填写人民币符号“￥”，阿拉伯小写金额数字要认真填写，不得连写分辨不清。

五、票据的出票日期必须使用中文大写，为防止变造票据的出票日期，在填写月、日时、月为壹、贰和壹拾的，日为壹至玖和壹拾、贰拾和叁拾的，应在其前加“零”，日为拾壹至拾玖的应在其前加“壹”，如1月15日应写成零壹月壹拾伍日，再如10月20日应写成零壹拾月零贰拾日。

六、票据出票日期使用小写填写的，银行不予受理；大写日期未按要求规范填写的，银行可予受理，但由此造成损失的由出票人自行承担。

lnx的定义域和值域
y=lnx的定义域是x>0，值域是y∈R。

自然对数以常数e为底数的对数。记作lnN(N>0)。在物理学，生物学等自然科学中有重要的意义。一般表示方法为lnx。数学中也常见以logx表示自然对数。

常数e的含义是单位时间内，持续的翻倍增长所能达到的极限值。

自然对数的底e是由一个重要极限给出的。我们定义：当n趋于无穷大时，


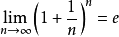
扩展资料

在1614年开始有对数概念，约翰·纳皮尔以及Jost Bürgi（英语：Jost Bürgi）在6年后，分别发表了独立编制的对数表，当时通过对接近1的底数的大量乘幂运算，来找到指定范围和精度的对数和所对应的真数，当时还没出现有理数幂的概念。

1742年William Jones才发表了幂指数概念。按后来人的观点，Jost
Bürgi的底数1.0001相当接近自然对数的底数e，而约翰·纳皮尔的底数0.99999999相当接近1/e。

实际上不需要做开高次方这种艰难运算，约翰·纳皮尔用了20年时间进行相当于数百万次乘法的计算，Henry
Briggs建议纳皮尔改用10为底数未果，他用自己的方法于1624年部份完成了常用对数表的编制。

1649年，Alphonse Antonio de Sarasa（英语：Alphonse Antonio de Sarasa）将双曲线下的面积解释为对数。

1、松鼠的尾巴像一把扫帚，可以扫地。

2、松鼠的尾巴像一个降落伞，帮助松鼠保持平衡安全落地。

3、松鼠的尾巴像一床棉被，松软而保温，可以帮助抵御寒冷。

4、松鼠的尾巴像一把雨伞，下雨时打开可以遮风挡雨。

5、松鼠的尾巴像一个鸡毛掸子，可以弹灰打扫卫生。

6、松鼠的尾巴像一个大大的感叹号。

7、松鼠的尾巴像小帆，翘起可以帮助游水。

8、松鼠的尾巴像时髦小伙的头发。

9、松鼠的尾巴像书法家手下的毛笔。

10、松鼠的尾巴像长满了软刺的仙人掌。

扩展资料：

松鼠的尾巴的作用：

1、松鼠的尾巴蓬松而巨大，可以帮助松鼠在树林间跳跃时保持平衡，控制方向，在被天敌猎杀时，可以快速逃命。

2、松鼠的尾巴在高出下落的过程中可以增加空气的阻力，降低下降的速度，保证松鼠的安全，起到降落伞的作用。

3、松鼠比较怕冷，而松鼠的大尾巴可以让其在寒冬中保持温度，让松鼠舒适的度过冬天。

4、危急时刻，松鼠会面对敌人，晃动大尾巴来迷惑敌人，类似于孔雀开屏吓走猎杀者一样。

5、松鼠的尾巴还起到同伴交流的作用，松鼠之间会通过尾巴摆动来交流信息。

6、通过查看松鼠的尾巴翘起的高低，就能很轻松的辨别松鼠的地位，比如说，松鼠首领喜欢将尾巴放的很低，而地位低的松鼠却喜欢把尾巴高高翘起。